Moscow Mathematics Festival 2009 - Grade 7. Time: 2 hours
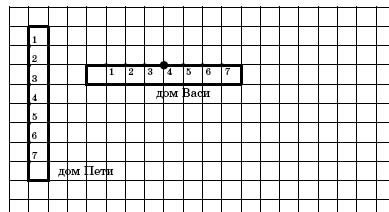
Problem 1.Petya and Vasya live in next-door apartment buildings (see map). Vasyalives in the fourth section of the building in which he lives. We know that Petya, inorder to follow a shortest path from his place to Vasya’s (not necessarily along the lines of the grid), can walk around the building where he (Petya) lives in eitherdirection. Determine in which section Petya lives. (5 points)
Problem 2. In each of two parcels Grandpa planted the same number of turnips.Each time the granddaughter visits then she pulls up 1/3 of the turnips in a parcel.Each time the dog shows up it pulls up 1/7 of the turnips in a parcel. And each time Misha visits he pulls up 1/12 of the turnips in a parcel. At the end of a week 7 turnips remained in the first parcel, and at the end of the second week 4 turnips. Did the dog ever show up in the second parcel? Note: The number of turnips pulled/remaining must always be a whole number. (5 points)
Problem 3. King Neptune is served by octopi with six, seven or eight legs. Those who have 7 always lie and those with 6 or 8 legs always tell the truth. Four octopi gottogether. The blue octopus said “we have 28 legs in total”, the green “we have 27legs in total”, the yellow “we have 26 legs in total” and the red “we have 25 legs intotal”. How many legs does each octopus have? (5 points) Problem 4. A stingy knight kept golden coins in 77 chests. Once, when he countedthe coins, he noticed that if one opened any two chests then it was possible todistribute the coins evenly between the two chests. He also noticed that if one opened any three, four, five… or 76 chests then it was also possible to divide thecoins in those evenly among the open chests. Suddenly there was a knock on thedoor, and the old miser did not know whether it was possible to distribute all thecoins evenly among all 77 chests. Is it possible to answer this question withoutlooking in the chests? (6 points)
